Exemple de Amos Judd

Ce problème a été posé par Lewis Carroll de la façon suivante:

1. Tous les agents de police du secteur dînent avec notre cuisinière ;
2. Amos Judd n'a jamais fait de séjour en prison ;
3. Les ``cousins'' de notre cuisinière aiment tous le gigot froid ;
4. Les hommes aux cheveux courts ont tous fait un séjour en prison ;
5. Tout homme aux cheveux longs est poète ;
6. Seuls les agents de police du secteur sont poètes ;
7. Seuls ses ``cousins'' dînent avec notre cuisinière.

Que peut-on dire sur Amos Judd ?

Formalisation

Pour résoudre ce problème, Lewis Carroll propose la méthode suivante:

1. ``normaliser'' le discours, c'est à dire reformuler chaque phrase (appelée ``proposition'') en utilisant un des schémas suivants:

   - Tout A est un B ;
   - Aucun A n'est un B ;
   - Seuls les A sont des B ;
   - Quelques A sont des B.

   où A et B sont des groupes nominaux qui désignent des catégories, c'est à dire des ensembles d'individus (l'ensemble des ``agents de police du secteur'', l'ensemble des ``hommes qui dînent avec notre cuisinière'', ...).

2. définir les catégories complémentaires: étant donnée une catégorie A, comp(A) désigne l'ensemble des individus n'appartenant pas à A. Par exemple,

   comp(``hommes aux cheveux courts'') = ``hommes aux cheveux longs'',
   comp(``poètes'') = ``hommes qui ne sont pas poètes''

   Remarque: comp(comp(A)) = A.

3. appliquer les ``syllogismes'' suivants pour déduire de nouvelles propositions:
   • SI aucun A n'est un C ET aucun B n'est un comp(C)
     ALORS aucun A n'est un B.

   • SI aucun A n'est un C ET aucun B n'est un C ET il existe au moins un C
     ALORS quelques comp(A) sont des comp(B).

   • SI aucun A n'est un C ET quelques B sont des C
     ALORS quelques comp(A) sont des B.

   On peut utiliser par ailleurs les propriétés suivantes sur les propositions:

   - quelques A sont des B 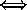quelques B sont des A ;
   - quelques A sont des B 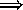il existe au moins un A ;
   - aucun A n'est un B 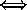aucun B n'est un A ;
   - aucun A n'est un B 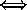Tout A est un comp(B) ;
   - aucun A n'est un 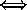B Seuls les comp(A) sont des B.